Binary tree level order traversal (20250724)

Question:
- Binary Tree Level Order Traversal
- Given a binary tree root, return the level order traversal of it as a nested list, where each sublist contains the values of nodes at a particular level in the tree, from left to right.
- Example 1:
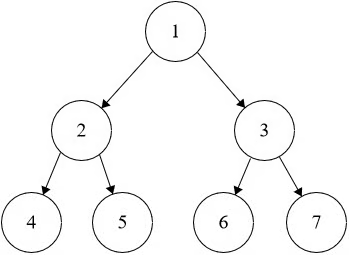
  - Input: root = [1,2,3,4,5,6,7] Output: [[1],[2,3],[4,5,6,7]]
- Example 2:
```
  Input: root = [1]
  Output: [[1]]
```
- Example 3:
```
  Input: root = []
  Output: []
```
- Constraints:
```
  0 <= The number of nodes in the tree <= 1000.
  -1000 <= Node.val <= 1000
```
Recommended Time & Space Complexity

You should aim for a solution with O(n) time and O(n) space, where n is the number of nodes in the given tree.
Hint 1:

The level of a tree refers to the nodes that are at equal distance from the root node. Can you think of an algorithm that traverses the tree level by level, rather than going deeper into the tree?

Solution 1: Travel tree level by level

  # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, val=0, left=None, right=None):
  #         self.val = val
  #         self.left = left
  #         self.right = right

  class Solution:
      def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
    
          if root is None:
              return[]

          node_list = [root]      # space: O(w), w<=n
          output = []             # space: O(n)

          while True:
              level_values = []   # space: O(w), w<=n
              new_node_list = []  # space: O(w), w<=n

              for i in range(len(node_list)):
                  node = node_list[i]
                  level_values.append(node.val)

                  if node.left is not None:
                      new_node_list.append(node.left)
                  if node.right is not None:
                      new_node_list.append(node.right)
                
              output.append(level_values)

              if not new_node_list:
                  break

              node_list = new_node_list
            
          return output

Time complexity: O(n)
Space complexity: O(n)

Hint 2:

We can use the Breadth First Search (BFS) algorithm to traverse the tree level by level. BFS uses a queue data structure to achieve this. At each step of BFS, we only iterate over the queue up to its size at that step. Then, we take the left and right child pointers and add them to the queue. This allows us to explore all paths simultaneously.
Hint 3:

The number of times we iterate the queue corresponds to the number of levels in the tree. At each step, we pop all nodes from the queue for the current level and add them collectively to the resultant array. This ensures that we capture all nodes at each level of the tree.

Solution 2:

Solution on needcode.
Breadth First Search. ``` python # Definition for a binary tree node. # class TreeNode: # def init(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right

class Solution: def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]: result = []

      q = collections.deque()
      q.append(root)

      while q:
          qLen = len(q)
          level_val = []
          for i in range(qLen):
              node = q.popleft()
              if node:
                  level_val.append(node.val)
                  q.append(node.left)
                  q.append(node.right)
            
          if level_val:
              result.append(level_val)

      return result   ```

Solution 3:

Solution on needcode.
if len(result) == depth: 當len(result) == depth 表示是第一次碰到這個 level 的 node，並且 result 二階 array 的長度剛好少一格
result[depth].append(node.val) 因為每個 level 的 node 一定是由左至右被看見的，因此可以按照順序加進該 level 的二階 array 就好

  # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, val=0, left=None, right=None):
  #         self.val = val
  #         self.left = left
  #         self.right = right

  class Solution:
      def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
          result = []

          def dfs(node, depth):
              if not node:
                  return None
              if len(result) == depth:
                  result.append([])
                
              result[depth].append(node.val)
              dfs(node.left, depth + 1)
              dfs(node.ritht, depth + 1)

          dfs(root, 0)
            
          return result

Note: Depth First Search

Recursive DFS

 class TreeNode:
     def __init__(self, val=0, left=None, righ=None):
         self.val = val
         self.left = left
         self.right = right

 def dfs(node):
     if not node:
         return
     print(node.val)
     dfs(node.left)
     dfs(node.right)

Iterative DFS using Stack

 class TreeNode:
     def __init__(self, val=0, left=None, righ=None):
         self.val = val
         self.left = left
         self.right = right

 def dfs_iterative(root):
     if not root:
         return

     stack = [root]

     while stack:
         node = stack.pop()
         print(node.val)

         # 先 push 右邊，再 push 左邊（因為 stack 是後進先出）
         if node.right:
             stack.append(node.right)
         if node.left:
             stack.append(node.left)

Recursive DFS v.s. Iterative DFS
- Recursive DFS: Risk of overflow (Since using python call stack memory)
- Iterative DFS: No limit (Since using own stack = [] memory, so crash until system runs out of RAM) You’re almost there! Here’s a refined and clear version of your comparison:
- Recursive DFS
  - Uses the Python call stack (system-managed)
  - ❗ Risk of stack overflow for deep trees
  - ✅ Code is shorter and cleaner
  - 📌 Good for small to medium-depth trees
- Iterative DFS
  - Uses your own stack (e.g., stack = [])
  - ✅ Handles very deep trees without recursion limits
  - ⚙️ Code is a bit more complex
  - 💪 More robust in large-scale or production settings